Abschätzung der Ausbreitung und Aufhöhung des Sickerwassers unter einer Versickerungsanlage

Modellierung der Sickerwasseraufhöhung als Pyramidenstumpf

In einem interessanten Projekt in 2023 habe ich die Ausbreitung unter einer Rigolenversickerung näher betrachtet. Ein abgeändertes Beispiel für eine kleine Rigole sehen Sie unten.

Vorgehensweise

Ausgehend von einer Rigole mit voll gefülltem Speichervolumen wurde zunächst als erster Schritt mit der Sickerfläche unter der Basis der Rigole das Sickervolumen der ungesättigten Bodenschicht (gut durchlässiger Sand) bestimmt. Die vertikal bis zur Wasseroberfläche darunter reichende Versickerungszone der Höhe h wurde als rechteckiger Pyramidenstumpf angenommen, mit einer vergrößerten Grundfläche (Abmessung der oberen Deckfläche + h/2). Mit der Porosität wurde der Porenraum als Sand-Pyramidenvolumen berechnet und mit der Sickerhöhe h ein ggf. vorhandener Überstau bis in die Rigole festgestellt.

Im zweiten Schritt wurde das wässergefüllte Sandvolumen bei vollständiger Versickerung als konstant angenommen und dann die seitliche Reichweite in mehreren Schritten vergrößert, als horizontale Ausbreitung des Sickerwassers auf dem Wasserspiegel. Dabei verflacht sich der Pyramidenstumpf zum Rand hin linear abnehmend auf Null, mit einem Anstieg bis zur Deckfläche. Diese lineare Berechnung ist nur eine Annäherung.

In der Realität wird sich die Oberfläche der Sickerwasserausbreitung oben flach abgerundet gestalten und evtl. exponentiell zum Rand gegen Null abnehmen. Da die Ausbreitung auch radial in Kreis- bis Ellipsenform geschieht, besteht hierin auch eine Abweichung von der winkligen Pyramidengrundfläche. Die rundliche Form hat in der Realität bei gleicher Entfernung eine größere Grundfläche.

Berechnung der Sickerwasserausbreitung

Ein Beispiel für die Volumenberechnung des Pyramidenstumpfes mit Formel sehen Sie in den folgenden Abbildungen, hier für die Sickerzone unter der Rigole (Internetquelle: Onlinerechner).

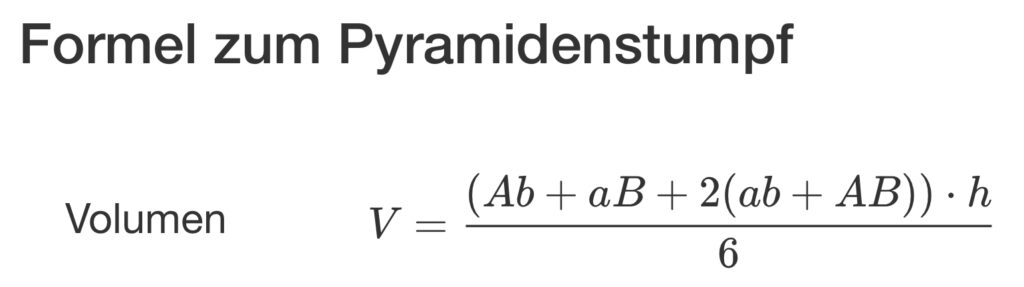
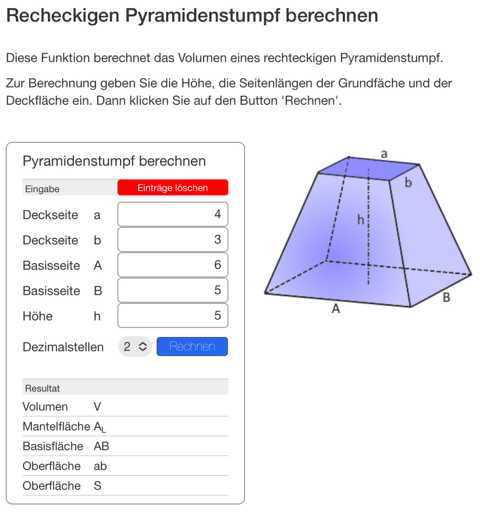
Beispielberechnung für eine kleine Rigole

Rigolenabmessungen einer Hohlkörperrigole aus 8 Blöcken (2 x 4 a. 0,80 m; 420 L)

• Breite 1,60 m
• Länge 3,20 m
• Höhe 0,66 m
• Speichervolumen 3,36 m³
• Sickerraum 1,20 m

Die Berechnung wurde mit zunehmenden Abständen zur Rigole in mehreren Schritten durchgeführt, wobei zunächst die Größe der Deckfläche beibehalten wurde. Die Daten und die Berechnung sind in der Tabelle abgebildet (als pdf öffnen). Im Diagramm ist die Abnahme der Aufhöhung als Deckfläche mit zunehmender Entfernung dargestellt. Bei 10 m Abstand zur Rigole beträgt sie 8,9 cm (blaue Kurve).

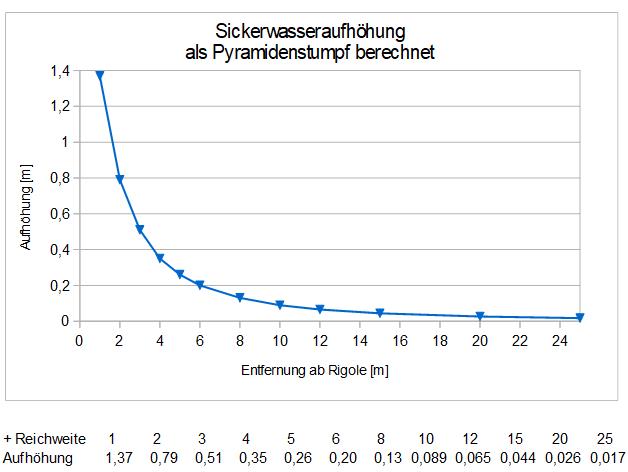
Vergrößert man die Deckfläche durch eine seitliche Versickerung, nimmt die Höhe anfangs auch stark ab und nähert sich bei größerer Grundfläche den Ausgangswerten an. Mit um 1 m allseitig erweiterter Deckfläche verringert sich die Höhe anfangs unter die Hälfte (grüne Kurve), bei 10 m Reichweite beträgt sie noch 6,9 cm.

Anzumerken ist immer bei diesem Modell: Zum Rand hin nimmt die Aufhöhung linear ab der Deckfläche auf 0 ab! Die Deckfläche wird als horizontale Fläche angenommen.

Berechnungsbeispiel für eine Hohlkörperrigole aus 2 x 4 Elementen a. 420 Liter Speichervolumen (V_R = 3,36 m³). Die Reichweite (Pyramidenbasis) wurde um 1,0 m bis auf 25,0 m allseitig ab der Rigole schrittweise erweitert.

Ein Beispiel für eine Modellierung der Ausbreitung und Aufhöhung mit einem Sickerwasserkörper als Kugelsegment folgt als Vergleich.

Im Ergebnis besteht bei größerer Ausbreitung kein wesentlicher Unterschied in der Aufhöhung. Die Modellierung als rechteckiger Pyramidenstumpf ist bei langgestreckten Rigolen bevorzugt anzuwenden, da die Geometrie hier eher vergleichbar ist.