Auswertung: Sickertest in einer kleinen Grube
Eine grafische Auswertemethode für den Sickertest
Hier folgt als Beispiel die Auswertung zur Ermittlung des kf-Wertes eines Sickertests in einer kleinen Grube in Diagrammform (meine bevorzugte Ausweremethode). Dadurch kann die Schwankung von Messwerten dargestellt, bewertet und ausgeglichen werden. Der kf-Wert kann dann i.d.R. aus dem gemittelten Endwert der letzten Messreihe festgelegt werden.
Der kf-Wert wird gemäß der Formel kf = Q / (t * Aw) [m/s] mit dem Zeitintervall t und den anderen Messgrößen berechnet.
Der Anfangswasserstand betrug 25 cm (2. Messreihe = 20 cm). Es wurde in Zeitabständen von 15 Minuten der Wasserstand mit einer Endabsenkung auf 12,0 bzw. 12,1 cm mit guter Übereinstimmung gemessen. In der Ergebnistabelle der Abbildung 1 sind die Daten aus der 2. Messreihe über 45 Minuten abgebildet und der kf-Wert daraus als Mittelwert berechnet (kf-Wert = 1,2*10-5 m/s). Dies ist möglich, wenn sich die Absenkung wie abgebildet nur noch geringfügig ändert.

Abbildung 1: Tabelle mit Daten und Messwerten der Onlineberechnung
Das folgende Diagramm zeigt die Auswertung der beiden Messreihen (60 und 45 min.): kf-Wert = 1,2*10-5 m/s (gemittelter Endwert der 2. Messreihe). Die letzten 3 Ergebnisse der 1. Messreihe wurden mit der 2. Messreihe bestätigt. Mit Berücksichtigung der seitlichen Versickerungsflächen bei jeder berechneten mittleren Druckhöhe während dieser Messungen wird im Diagramm für jeden Messpunkt der berechnete kf-Wert dargestellt.
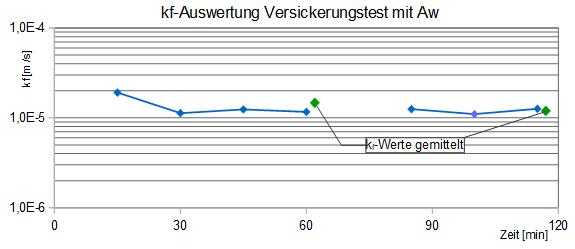
Abbildung 2: Diagrammauswertung eines Sickertests
Der Mittelwert der 1. Messreihe (grün) liegt zu hoch (ca. 23 % über Endwert), was durch den höheren 1. Messpunkt bedingt ist (ca. 60 % erhöht). Nur mit der 2. Messreihe ist eine Mittelwertbildung bei geringen Schwankungen der Einzelwerte möglich. Die Schwankung liegt im Bereich des Ablesefehlers des Wasserstandes (Abweichung bei 1 mm ca. 5 – 8 %). Bei möglichst genauer Herstellung und Messung der Grubenabmessungen liegt der Fehlerbereich in der daraus berechneten Wassermenge unterhalb von 5 %. Die Summe der möglichen Fehlerabweichung dürfte dabei im Bereich von 10 % liegen.
Gleichzeitig zeigt das Diagramm, dass die Mittelwertbildung über schwankende oder stark abweichende Messwerte einer oder mehrerer Messreihen problematisch ist und zu falschen Ergebnissen führen kann. Die Diagrammdarstellung ermöglicht eine gute Abbildung aller Messwerte und deren Bewertung.
